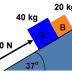
Contoh soal dan pembahasan dinamika gerak benda pada jalan berbentuk tikungan melingkar atau setengah melingkar dibahas di kelas 11 SMA.
Mencakup kecepatan maksimum yang diijinkan untuk benda (seperti mobil atau kendaraan) yang bergerak melingkar pada tipe jalan menikung kasar, tikungan miring licin dan tikungan miring kasar.
A. Rumus Kecepatan Maksimum Gerak Benda pada Beberapa Jenis Tikungan
Tipe 1 Tikungan Datar dan Kasar
Kecepatan maksimum yang diperbolehkan / roda kendaraan tidak slip:
dengan :
Vmaks = kecepatan maksimum yang diperbolehkan (m/s)
g = percepatan gravitasi bumi (m/s2)
μs = kefisien gesekan statis
r = jari-jari / radius tikungan jalan (m )
Tipe 2 Tikungan Miring dan Licin

Kecepatan maksimum yang diperbolehkan / roda kendaraan tidak slip:

dengan :
Vmaks = kecepatan maksimum yang diperbolehkan (m/s)
g = percepatan gravitasi bumi (m/s2)
θ = sudut kemiringan jalan terhadap garis mendatar
Tipe 3 Tikungan Miring dan Kasar

Kecepatan maksimum yang diperbolehkan / roda kendaraan tidak slip:

dengan :
Vmaks = kecepatan maksimum yang diperbolehkan (m/s)
g = percepatan gravitasi bumi (m/s2)
θ = sudut kemiringan jalan terhadap garis mendatar
B. Contoh Soal dan Pembahasan
Soal No. 1
Sebuah mobil bergerak pada suatu tikungan datar dan kasar. Jika jari-jari tikungan 50 m, koefisien gesekan statis jalan 0,3 dan percepatan gravitasi bumi 9,8 m/s2 tentukan kecepatan maksimum mobil saat berada di tikungan tersebut!
Pembahasan

Soal No. 2
Untuk merancang sebuah tikungan agar bisa dilalui dengan aman kendaraan yang melaju dengan kecepatan 20 m/s dengan koefisien gesekan jalan 0,25 tentukan jari-jari tikungan tersebut! (g = 10 m/s2)
Pembahasan

Soal No. 3
Sebuah tikungan miring dengan jari-jari 30 m dapat dilalui dengan aman pada kecepatan maksimum 54 km/jam pada saat jalan tertutup salju. Tentukan sudut kemiringan jalan tersebut!
Pembahasan
Anggap saat jalan tertutup salju tidak ada gesekan antara jalan dan roda kendaraan, 54 km/jam = 15 m/s

Soal No. 4
Sebuah tikungan miring yang licin memiliki radius 40√3 m. Jika kemiringan badan jalan adalah 30o dan percepatan gravitasi 10 m/s2 tentukan kecepatan maksimum yang diijinkan saat melalui tikungan tersebut!
Pembahasan

Soal No. 5
Berapakah kecepatan maksimum yang diijinkan saat sebuah mobil melewati suatu tikungan miring yang kasar jika radius tikungan 26 m, koefisien gesekan jalan 0,25 dan sudut kemiringan jalan adalah 37o?
Pembahasan

Soal No. 6
Tikungan miring dengan jari-jari 50 m memiliki permukaan jalan yang kasar dengan koefisien gesekan sebesar 2/7. Jika tikungan dirancang dapat dilewati kendaraan dengan kecepatan maksimum 108 km/jam, tentukan sudut kemiringan tikungan tersebut!
Pembahasan
Jalan miring kasar, 108 km/jam = 30 m/s

(Sekedar soal ya,...jangan bayangkan banyak jalan dibuat dengan kemiringan 45o!!)
C. Penurunan Rumus
Berikut cara mendapatkan rumus untuk Tipe Tikungan Miring dan Kasar seperti soal nomor 5 atau nomor 6:

Gaya-gaya yang bekerja pada mobil ada 3:
1) gaya normal atau N
2) gaya berat atau w, dimana nanti w = mg
3) gaya gesek atau f, di sini gaya geseknya adalah gaya gesek statis
Langkah berikutnya gaya normal N kita uraikan menjadi komponen-komponennya, juga gaya gesek diuraikan seperti terlihat pada gambar berikut.

Berikutnya hukum newton untuk gerak melingkar, gaya-gaya yang digunakan hanya gaya yang berarah menuju pusat lingkaran atau meninggalkan pusat lingkaran (dalam kasus ini sama dengan gaya yang arahnya lurus ke kanan atau lurus ke kiri), di sini hanya ada gaya yang menuju pusat saja:

Persamaan (1)
Dari gaya-gaya pada sumbu y, pada kasus ini sama dengan gaya yang arahnya ke atas atau ke bawah:

Persamaan (2)
Gabungkan persamaan 1 dan 2, coret N dan m nya:

Atur lagi yang bagus

sin θ / cos θ tidak lain adalah tan θ sehingga

Kecepatan maksimum yang diperbolehkan / roda kendaraan tidak slip:
dengan :
Vmaks = kecepatan maksimum yang diperbolehkan (m/s)
g = percepatan gravitasi bumi (m/s2)
θ = sudut kemiringan jalan terhadap garis mendatar
Tipe 3 Tikungan Miring dan Kasar
Kecepatan maksimum yang diperbolehkan / roda kendaraan tidak slip:
dengan :
Vmaks = kecepatan maksimum yang diperbolehkan (m/s)
g = percepatan gravitasi bumi (m/s2)
θ = sudut kemiringan jalan terhadap garis mendatar
B. Contoh Soal dan Pembahasan
Soal No. 1
Sebuah mobil bergerak pada suatu tikungan datar dan kasar. Jika jari-jari tikungan 50 m, koefisien gesekan statis jalan 0,3 dan percepatan gravitasi bumi 9,8 m/s2 tentukan kecepatan maksimum mobil saat berada di tikungan tersebut!
Pembahasan
Soal No. 2
Untuk merancang sebuah tikungan agar bisa dilalui dengan aman kendaraan yang melaju dengan kecepatan 20 m/s dengan koefisien gesekan jalan 0,25 tentukan jari-jari tikungan tersebut! (g = 10 m/s2)
Pembahasan
Soal No. 3
Sebuah tikungan miring dengan jari-jari 30 m dapat dilalui dengan aman pada kecepatan maksimum 54 km/jam pada saat jalan tertutup salju. Tentukan sudut kemiringan jalan tersebut!
Pembahasan
Anggap saat jalan tertutup salju tidak ada gesekan antara jalan dan roda kendaraan, 54 km/jam = 15 m/s
Soal No. 4
Sebuah tikungan miring yang licin memiliki radius 40√3 m. Jika kemiringan badan jalan adalah 30o dan percepatan gravitasi 10 m/s2 tentukan kecepatan maksimum yang diijinkan saat melalui tikungan tersebut!
Pembahasan
Soal No. 5
Berapakah kecepatan maksimum yang diijinkan saat sebuah mobil melewati suatu tikungan miring yang kasar jika radius tikungan 26 m, koefisien gesekan jalan 0,25 dan sudut kemiringan jalan adalah 37o?
Pembahasan
Soal No. 6
Tikungan miring dengan jari-jari 50 m memiliki permukaan jalan yang kasar dengan koefisien gesekan sebesar 2/7. Jika tikungan dirancang dapat dilewati kendaraan dengan kecepatan maksimum 108 km/jam, tentukan sudut kemiringan tikungan tersebut!
Pembahasan
Jalan miring kasar, 108 km/jam = 30 m/s
(Sekedar soal ya,...jangan bayangkan banyak jalan dibuat dengan kemiringan 45o!!)
C. Penurunan Rumus
Berikut cara mendapatkan rumus untuk Tipe Tikungan Miring dan Kasar seperti soal nomor 5 atau nomor 6:
Gaya-gaya yang bekerja pada mobil ada 3:
1) gaya normal atau N
2) gaya berat atau w, dimana nanti w = mg
3) gaya gesek atau f, di sini gaya geseknya adalah gaya gesek statis
Langkah berikutnya gaya normal N kita uraikan menjadi komponen-komponennya, juga gaya gesek diuraikan seperti terlihat pada gambar berikut.
Berikutnya hukum newton untuk gerak melingkar, gaya-gaya yang digunakan hanya gaya yang berarah menuju pusat lingkaran atau meninggalkan pusat lingkaran (dalam kasus ini sama dengan gaya yang arahnya lurus ke kanan atau lurus ke kiri), di sini hanya ada gaya yang menuju pusat saja:
Persamaan (1)
Dari gaya-gaya pada sumbu y, pada kasus ini sama dengan gaya yang arahnya ke atas atau ke bawah:
Persamaan (2)
Gabungkan persamaan 1 dan 2, coret N dan m nya:
Atur lagi yang bagus
sin θ / cos θ tidak lain adalah tan θ sehingga